I've decided to move to WordPress instead of blogger, because it seems to be faster, no Google+ integration is required (only reason I have a Google+ account is for Blogger) and inline LaTeX code seems to work. I also prefer the themes available on WordPress to Blogger too.
I've transferred all my posts, links and comments to WordPress. This is actually the second move for this blog, where it originated as a basic HTML website with a poor hosting provider. I then had to rewrite all my webpages for that website onto blogger. Thankfully, an Import/Export feature is supported between Blogger and WordPress!
WordPress URL - https://bsodtutorials.wordpress.com/
BSODTutorials
Windows Internals, System Security, Theoretical Computer Science and Debugging.
Friday, 12 September 2014
WinDbg Commands and Extensions - SwishDbgExt Library
The SwishDbgExt library contains a number of interesting extensions which are imperative for deep debugging results. The SwishDbgExt library was written by Matt Suiche.
Note: If you wish to use the ProcDumpExt DLL for WinDbg, and also view the help information for the extensions provided in SwishDbgExt, then you'll need to unload ProcDumpExt first since ProcDumpExt will overload the !help extension with it's own version. You can simply load ProcDumpExt again afterwards. Alternatively, if you do not wish to unload the ProcDumpExt DLL, then simply use the longhand method of !SwishDbgExt.help <SwishDbgExt Extension>.
You must also omit the exclamation mark (!) from the extension name, otherwise the !help extension will not work.
Note: You can use the .chain command to check if you have the ProcDumpExt DLL loaded or not. The .chain command will dump all loaded DLLs for the dump file.
The available extensions from the DLL can be found by using the !SwishDbgExt.help extension without any extensions added.
I will provide a quick overview for the extensions which can be used with SwishDbgExt.
!ms_drivers:
The !ms_drivers extension is basically the same as the lm or lmnst command. There are some additional parameters you can add to the !ms_drivers extension to spice up the command.
IRP Hooking involves a hook within the array stored within the DRIVER_OBJECT structure, this array or table of IRP_MJ_ functions is hooked and the code responsible for the IRP is redirected to malicious code. Please note hooking is used for legitimate processes such as debugging and patch releases.
!ms_gdt
The !ms_gdt extension can be used to view the GDT and LDT within the GDT. The GDT is public for all processes, whereas, the LDT is designed to be private for a specific process.
!ms_ssdt
The !ms_ssdt extension will dump the SSDT and if any functions have been patched or hooked. Remember that hooking the SSDT is used by legitimate programs, and most modern rootkits tend to do not use this method anymore.
!ms_idt
The !ms_idt extension is the same as the traditional !idt extension but with the added feature of detecting hooks within the dump file.
!ms_timers
I wouldn't consider the !ms_timers as a replacement for !timer, however, it is a great extension for being used to conjunction with the WinDbg !timer extension. The !ms_timers can detect hooking within the _KTIMER_TABLE.
Note: If you wish to use the ProcDumpExt DLL for WinDbg, and also view the help information for the extensions provided in SwishDbgExt, then you'll need to unload ProcDumpExt first since ProcDumpExt will overload the !help extension with it's own version. You can simply load ProcDumpExt again afterwards. Alternatively, if you do not wish to unload the ProcDumpExt DLL, then simply use the longhand method of !SwishDbgExt.help <SwishDbgExt Extension>.
You must also omit the exclamation mark (!) from the extension name, otherwise the !help extension will not work.
Note: You can use the .chain command to check if you have the ProcDumpExt DLL loaded or not. The .chain command will dump all loaded DLLs for the dump file.
The available extensions from the DLL can be found by using the !SwishDbgExt.help extension without any extensions added.
I will provide a quick overview for the extensions which can be used with SwishDbgExt.
!ms_drivers:
The !ms_drivers extension is basically the same as the lm or lmnst command. There are some additional parameters you can add to the !ms_drivers extension to spice up the command.
The !ms_drivers /scan extension can be used to find drivers using IRP Hooking.
IRP Hooking involves a hook within the array stored within the DRIVER_OBJECT structure, this array or table of IRP_MJ_ functions is hooked and the code responsible for the IRP is redirected to malicious code. Please note hooking is used for legitimate processes such as debugging and patch releases.
!ms_gdt
The !ms_gdt extension can be used to view the GDT and LDT within the GDT. The GDT is public for all processes, whereas, the LDT is designed to be private for a specific process.
!ms_ssdt
The !ms_ssdt extension will dump the SSDT and if any functions have been patched or hooked. Remember that hooking the SSDT is used by legitimate programs, and most modern rootkits tend to do not use this method anymore.
!ms_idt
The !ms_idt extension is the same as the traditional !idt extension but with the added feature of detecting hooks within the dump file.
!ms_timers
I wouldn't consider the !ms_timers as a replacement for !timer, however, it is a great extension for being used to conjunction with the WinDbg !timer extension. The !ms_timers can detect hooking within the _KTIMER_TABLE.
Saturday, 30 August 2014
Some Interesting Numbers - Kaprekar's Constant, Polygonal Numbers and Highly Composite Numbers
I thought I would wrote a small article on some numbers which I find interesting, I may expand upon this topic in the future, but for this article I'm going to restrict myself to three forms of number: Kaprekar's Constant, Polygonal Numbers and Highly Composite Numbers.
Kaprekar's Constant:
Kaprekar's Constant is a special constant discovered by the Indian Mathematician called D.R.Kaprekar. The constant has the value of 6174. The constant comes from a simple algorithm known as Kaprekar's Routine. The constant can be produced from at most 7 iterations.
Kaprekar's Constant will always be produced after iterating through Kaprekar's Routine, when given an arbitrary 4 digit integer, providing that at least two of the digits are different otherwise the constant will not be produced.
For example, using 3524 from Wikipedia (since the number of steps is knowingly small), arrange the number in descending order and then ascending order. Subtract these two numbers, and then repeat the process until you reach 6174. You may add any leading 0's to maintain a four digit number.
5432 - 2345 = 3087
8730 - 0378 = 8532
8532 - 2358 = 6174
7641 - 1467 = 6174
Polygonal Numbers:
Polygonal Numbers when arranged as dots will form a polygon like a triangle or square. The Polygonal Numbers usually have a simple formula associated with them.
The first Hexagonal numbers are given as follows:
The general formula for any s-sided polygonal number can be given by the following:
$$P(S,N) = \frac{n^2(s - 2) - n(s-4)}{2}$$
For any given s-sided polygonal number, whereby P(S,N) = X, then the nth term number for X can be found using the following formula:
$$n = \frac{\sqrt{8(s -2) x +(s-4)^2} + (s-4)}{2(s-2)}$$
Highly Composite Numbers:
Highly Composite Numbers are a infinite sequence of numbers with the property, that the number of divisors is greater than any smaller n (any smaller number).
The first Highly Composite Numbers (HCN) are as listed below:
1, 2, 4, 6, 12, 24, 36, 48,...
For example, the number of divisors for 24 is 8, and the all the numbers below 24, have a number of divisors which is not greater than 8 and therefore 24 is considered to be a Highly Composite Number.
There some interesting properties related to Highly Composite Numbers which can be found in the References section.
References:
Highly Composite Number - Wikipedia
Highly Composite Number
Table of Divisors
6174 - Wikipedia
Polygonal Number
Polygonal Number - Wikipedia
Kaprekar's Constant:
Kaprekar's Constant is a special constant discovered by the Indian Mathematician called D.R.Kaprekar. The constant has the value of 6174. The constant comes from a simple algorithm known as Kaprekar's Routine. The constant can be produced from at most 7 iterations.
Kaprekar's Constant will always be produced after iterating through Kaprekar's Routine, when given an arbitrary 4 digit integer, providing that at least two of the digits are different otherwise the constant will not be produced.
For example, using 3524 from Wikipedia (since the number of steps is knowingly small), arrange the number in descending order and then ascending order. Subtract these two numbers, and then repeat the process until you reach 6174. You may add any leading 0's to maintain a four digit number.
5432 - 2345 = 3087
8730 - 0378 = 8532
8532 - 2358 = 6174
7641 - 1467 = 6174
Polygonal Numbers:
Polygonal Numbers when arranged as dots will form a polygon like a triangle or square. The Polygonal Numbers usually have a simple formula associated with them.
The first Hexagonal numbers are given as follows:
The general formula for any s-sided polygonal number can be given by the following:
$$P(S,N) = \frac{n^2(s - 2) - n(s-4)}{2}$$
For any given s-sided polygonal number, whereby P(S,N) = X, then the nth term number for X can be found using the following formula:
$$n = \frac{\sqrt{8(s -2) x +(s-4)^2} + (s-4)}{2(s-2)}$$
Highly Composite Numbers:
Highly Composite Numbers are a infinite sequence of numbers with the property, that the number of divisors is greater than any smaller n (any smaller number).
The first Highly Composite Numbers (HCN) are as listed below:
1, 2, 4, 6, 12, 24, 36, 48,...
For example, the number of divisors for 24 is 8, and the all the numbers below 24, have a number of divisors which is not greater than 8 and therefore 24 is considered to be a Highly Composite Number.
There some interesting properties related to Highly Composite Numbers which can be found in the References section.
References:
Highly Composite Number - Wikipedia
Highly Composite Number
Table of Divisors
6174 - Wikipedia
Polygonal Number
Polygonal Number - Wikipedia
Tuesday, 19 August 2014
Chromatic Properties of House and House X Graphs
As with Bull Graphs, House Graphs are simple graphs (not the Graph Theoretic definition) which have been neglected. They may not be interesting or yield any important findings to professional research mathematicians, but I haven't been able to find a paper or website which lists or shows any of the House Graphs properly at all. My intention is simply to state and prove of these properties.
Please note I'm not a professional mathematician and I'm not even studying for a Mathematics degree (Computer Science), and therefore may make mistakes or misunderstandings.
There are two main variants of House Graphs, and in this article I will listing the Vertex Colouring and Edge Colouring properties of such graphs. The two graphs are the House Graph and the House-X Graph.
Please note I'm not a professional mathematician and I'm not even studying for a Mathematics degree (Computer Science), and therefore may make mistakes or misunderstandings.
There are two main variants of House Graphs, and in this article I will listing the Vertex Colouring and Edge Colouring properties of such graphs. The two graphs are the House Graph and the House-X Graph.
 |
| House Graph |
 |
| House-X Graph |
Both of the graphs are simple graphs, and the same number of vertices. In terms of the structure of the graph, the only difference between the graphs are the number of edges. The number edges for the House Graph is 6 and the number of edges for the House-X Graph is 8. The number of edges will be fundamental to the chromatic properties of these graphs.
Chromatic Number:
The Chromatic Number is defined to be the minimum vertex colouring of a graph G. $$\chi(G)$$ is the common notation for the chromatic number of a given graph called G. The minimum vertex colouring is the smallest number of k-colours needed to colour the vertices, so that no two adjacent vertices contain the same colour; no two vertices connected by a common edge have the same vertex colour.
The chromatic number of a House X Graph is 4, this is very obvious, because the chromatic number of a complete graph with n vertices is n. The House-X Graph contains a complete graph of 4 vertices, and the addition of a 'isolated' single vertex creates a chromatic number of 4.
The chromatic number of the House Graph is 3, for a one main reason, the 3-Complete Graph is a subgraph of the House Graph which leads to the fact at least three colours to required. This isn't really a rigorous proof as such, but by attempting to colour the graph with only 2 colours, the idea will become more apparent.
Chromatic Index:
The Chromatic Index of a graph is defined to be the minimum edge colouring of a graph G. The edge colouring of a graph, is when two or more edges incident to a common vertex do not share the same edge colour. Since the House-X Graph and the House Graph are both simple graphs, then Vizing's Theorem can be applied here to show the chromatic index of both graphs.
Vizing's Theorem states that the minimum number of colours needed to edge colour a graph is the maximum degree or the maximum degree with the addition of 1. The maximum degree of a graph is the largest degree of a vertex within the graph. The degree is the number of edges incident to that vertex.
The House Graph has a chromatic index of 3, and the House-X Graph has a chromatic index of 4. The chromatic index for the House Graph is mostly due to the 3-Complete Graph being present as a subgraph, and the fact that Complete Graphs on odd n vertices will have a chromatic index of n.
Reference(s):
Saturday, 9 August 2014
Windows Access Tokens - !token and _TOKEN
Windows needs to ensure that untrusted code and untrusted users aren't accessing important areas of the operating system, and creating problems which would ultimately lead to a vast number of BSODs.
Windows manages this through Access Tokens which are used to identify the security context of a process/thread and a user. Access Tokens take two main forms: a Primary access token and a Impersonation access token. The Access Token additionally has two important features which are integral to security validation: SIDs (Security Identifiers) and a Privilege Array which contains the privileges allowed for that object.
The token type can be found within a enumeration called TOKEN_TYPE.
The data structure can be found under the TokenType field within the _TOKEN structure. The Primary type determines the security context of the process for the currently logged on user, and the Impersonation type allows a thread to temporarily use a different security context.
The Token type can also be found using the !token extension:
We can view the Privilege Array within WinDbg, by using the !token extension with the address of the access token for a given process, the Privilege Array can be seen below:
As mentioned before, the SID is used to determine if a thread or process has access to an object, and the privilege array will determine what that process or thread is able to do with that object. For example, being able to read and write to a file object.
SIDs have a unique format, and each segment will provide some useful identity information. Each SID will be stored with a _SID data structure as shown below:
These fields can be found within a SID, for which I will demonstrate in a moment. Each SID will have a S prefix. If you know the address of a SID, then you can use the !sid extension to translate the address into the appropriate SID.
The three numbers in yellow, and in preceding in chronological order, represent the use of the SID, the revision number and identifier authority. The blue represents the sub-authorities and the green represents the RID or relative identifier.
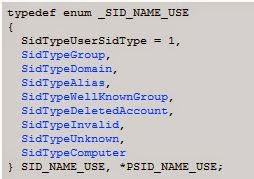
The SID use can be found within an enumeration called SID_NAME_USE. The 1 indicates that this is a User SID.
The sub-authorities belong to the identifier authority, and used for more unique identification. The identifier authority or issuing authority tends to be Windows.
The relative identifier is used to identify the SID in relation to the issuing authority. Each unique user or group will start at 1000, and for each new user or group, then this number be incremented by 1, therefore there is at least two users on this system. Administrators are typically given 500 and Guest accounts are given 501.
Primary and Impersonation Tokens have two subtypes: Restricted Tokens and Filtered Admin Token. A Restricted Token is derived from another access token with the following limitations:
I will conclude this article by describing some of the more interesting and helpful fields within the _TOKEN data structure.
TokenSource - The _TOKEN_SOURCE structure provides a information pretaining to the soruce of the access token. This can be the RPC server, Session Manager or LAN Manager.
TokenID, ParentTokenID and AuthenticationId - The Locally Unique Identifier (_LUID) is used to uniquely identify a access token from the many other potiental access tokens being used on the system. See the _TOKEN_CONTROL data structure for more information.
Privileges - The _SEP_TOKEN_PRIVILEGES structure contains the array of privileges related to the access token.
TokenType - The _TOKEN_TYPE shows if the access token is a primary or impersonation token.
ImpersonationLevel - The _SECURITY_IMPERSONATION_LEVEL is an enumeration of impersonation levels for the impersonation token. There is four different impersonation levels.
TokenFlags - This field contains any flags which have been set for the access token.
TokenInUse - Shows if the access token is currently being used.
SidHash, RestrictedSidHash - These two hashes for the SID have been added to prevent token stealing. These hashes are checked each time the token is used.
References:
SID Components (Windows)
Access Tokens (Windows)
Restricted Tokens (Windows)
Impersonation Levels (Windows)
Windows manages this through Access Tokens which are used to identify the security context of a process/thread and a user. Access Tokens take two main forms: a Primary access token and a Impersonation access token. The Access Token additionally has two important features which are integral to security validation: SIDs (Security Identifiers) and a Privilege Array which contains the privileges allowed for that object.
The token type can be found within a enumeration called TOKEN_TYPE.
The data structure can be found under the TokenType field within the _TOKEN structure. The Primary type determines the security context of the process for the currently logged on user, and the Impersonation type allows a thread to temporarily use a different security context.
The Token type can also be found using the !token extension:
We can view the Privilege Array within WinDbg, by using the !token extension with the address of the access token for a given process, the Privilege Array can be seen below:
As mentioned before, the SID is used to determine if a thread or process has access to an object, and the privilege array will determine what that process or thread is able to do with that object. For example, being able to read and write to a file object.
SIDs have a unique format, and each segment will provide some useful identity information. Each SID will be stored with a _SID data structure as shown below:
These fields can be found within a SID, for which I will demonstrate in a moment. Each SID will have a S prefix. If you know the address of a SID, then you can use the !sid extension to translate the address into the appropriate SID.
The three numbers in yellow, and in preceding in chronological order, represent the use of the SID, the revision number and identifier authority. The blue represents the sub-authorities and the green represents the RID or relative identifier.
The SID use can be found within an enumeration called SID_NAME_USE. The 1 indicates that this is a User SID.
The sub-authorities belong to the identifier authority, and used for more unique identification. The identifier authority or issuing authority tends to be Windows.
The relative identifier is used to identify the SID in relation to the issuing authority. Each unique user or group will start at 1000, and for each new user or group, then this number be incremented by 1, therefore there is at least two users on this system. Administrators are typically given 500 and Guest accounts are given 501.
Primary and Impersonation Tokens have two subtypes: Restricted Tokens and Filtered Admin Token. A Restricted Token is derived from another access token with the following limitations:
- Privileges can be removed from the privilege array.
- The SIDs in the token can have their access altered.
I will conclude this article by describing some of the more interesting and helpful fields within the _TOKEN data structure.
TokenSource - The _TOKEN_SOURCE structure provides a information pretaining to the soruce of the access token. This can be the RPC server, Session Manager or LAN Manager.
TokenID, ParentTokenID and AuthenticationId - The Locally Unique Identifier (_LUID) is used to uniquely identify a access token from the many other potiental access tokens being used on the system. See the _TOKEN_CONTROL data structure for more information.
Privileges - The _SEP_TOKEN_PRIVILEGES structure contains the array of privileges related to the access token.
TokenType - The _TOKEN_TYPE shows if the access token is a primary or impersonation token.
ImpersonationLevel - The _SECURITY_IMPERSONATION_LEVEL is an enumeration of impersonation levels for the impersonation token. There is four different impersonation levels.
TokenFlags - This field contains any flags which have been set for the access token.
TokenInUse - Shows if the access token is currently being used.
SidHash, RestrictedSidHash - These two hashes for the SID have been added to prevent token stealing. These hashes are checked each time the token is used.
References:
SID Components (Windows)
Access Tokens (Windows)
Restricted Tokens (Windows)
Impersonation Levels (Windows)
Thursday, 31 July 2014
Windows Integrity Levels - Process Explorer and WinDbg
From Windows Vista onwards, Microsoft has placed a substantially greater focus on the security of the operating system, which is one of the areas most users will neglect and then later come to complain about. In this article I'm going to talk about Windows Integrity Levels, and how we can view this information in WinDbg and through some SysInternals Tools. In another article, I will going into more depth about access tokens and how they are used to increase system security.
These security measures were introduced since it was relatively easy to modify memory and remove any security identification, thus leads to code modification and injection being used to allow illegitimate access to important system data structures etc.
User-Mode processes often require the use of system services and system resources which reside within the Kernel-Mode. To stop any illegitimate access or any poor programming from creating havoc in Kernel-Mode, some security validation procedures have been introduced to Windows, these commonly are Integrity Levels and Access Tokens.
The Integrity Levels come in 5 different levels, with 4 being the highest and most privileged level.
Integrity Levels (Lowest to Highest):
Viewing Integrity Levels (Process Explorer):
If you haven't enabled the Integrity Level column in Process Explorer, then follow these simple steps:
Click View > Select Columns > Integrity Level > OK/Apply
Viewing Integrity Levels (WinDbg):
Alternatively, we can view the Integrity Level of a process with WinDbg, and the viewing the _TOKEN data structure. I'm not sure on its effectiveness.
These security measures were introduced since it was relatively easy to modify memory and remove any security identification, thus leads to code modification and injection being used to allow illegitimate access to important system data structures etc.
User-Mode processes often require the use of system services and system resources which reside within the Kernel-Mode. To stop any illegitimate access or any poor programming from creating havoc in Kernel-Mode, some security validation procedures have been introduced to Windows, these commonly are Integrity Levels and Access Tokens.
The Integrity Levels come in 5 different levels, with 4 being the highest and most privileged level.
Integrity Levels (Lowest to Highest):
- Untrusted (0) - Blocks most write access to a majority of objects
- Low (1) - Blocks most write access to registry keys and file objects
- Medium (2) - This is the default setting for most processes when UAC has been enabled on the system.
- High (3) - Most processes will have this setting if UAC is disabled and the currently logged on user is the administrator. Otherwise, administrative programs will have this setting with
- System (4) - This is a setting reserved for system level components.
Viewing Integrity Levels (Process Explorer):
If you haven't enabled the Integrity Level column in Process Explorer, then follow these simple steps:
Click View > Select Columns > Integrity Level > OK/Apply
 |
| Process Explorer |
Alternatively, we can view the Integrity Level of a process with WinDbg, and the viewing the _TOKEN data structure. I'm not sure on its effectiveness.
Using the Token Address with _TOKEN data structure, we can find the Integrity Level of the process.
Saturday, 19 July 2014
Discrete Geometry - Bin Packing Problem
This post is a little irrelevant to general contents of my blog, but I found this to be a interesting geometry problem and it does have some ties with Computational Geometry, which is form a of theoretical computer science. There is additionally some connection with Computational Complexity Theory too. The Bin Packing Problem isn't difficult to explain, and yet can be difficult to find a optimal solution.
With Discrete Mathematics, I personally find that the branches within this field are more accessible but the problems are difficult enough to be interesting and form a field of serious mathematical study. I'm only a amateur mathematician and a student, so if there are any problems then please highlight them in the comments section.
Bin Packing Problem:
The Bin Packing Problem is an example of a optimization problem which has a surprisingly large number of applications, especially in logistics and data management. The Bin Packing Problem asks to minimize the number of bins needed to pack a certain number and given volume for a list of objects. These objects can vary in size, but the bin volumes will remain fixed. There are some programs which will give valid suggestions for the most optimal method, however, the problem is a NP- Hard Combinatorial class type.
The sum of the sizes of the items must be less than or equal to the total volume of the bins being used. The size of the items can never be greater than the total volume of the bins. If the volume of one bin is reached, then a new bin will need to be used. The problem looks to find a packing method which will reduce the number of bins needed to provide a optimal method.
The First-Fit Algorithm is the best algorithm which has been used for the bin packing problem. The First-Fit Algorithm is an example of a greedy approximation algorithm, in that the items will processed in any given order. The algorithm will place as many items as possible into the first bin, and then create a new bin if no other additional bins can be found. The process is then repeated for the rest of the items.
The First-Fit Algorithm has a approximation factor of 2 (APX). The approximation factor is used for NP-Hard problems, since it is very unlikely that a efficient algorithm will be produced to solve the problem directly, and therefore a P class algorithm can be developed in order to find a approximate answer. The approximation factor of 2, means that the algorithm will never use more than twice the number of least bins needed for the bin packing problem. For instance, if the number of bins needed was 2, then the algorithm will never use more than 4.
References:
Bin Packing Problem
With Discrete Mathematics, I personally find that the branches within this field are more accessible but the problems are difficult enough to be interesting and form a field of serious mathematical study. I'm only a amateur mathematician and a student, so if there are any problems then please highlight them in the comments section.
Bin Packing Problem:
The Bin Packing Problem is an example of a optimization problem which has a surprisingly large number of applications, especially in logistics and data management. The Bin Packing Problem asks to minimize the number of bins needed to pack a certain number and given volume for a list of objects. These objects can vary in size, but the bin volumes will remain fixed. There are some programs which will give valid suggestions for the most optimal method, however, the problem is a NP- Hard Combinatorial class type.
The sum of the sizes of the items must be less than or equal to the total volume of the bins being used. The size of the items can never be greater than the total volume of the bins. If the volume of one bin is reached, then a new bin will need to be used. The problem looks to find a packing method which will reduce the number of bins needed to provide a optimal method.
The First-Fit Algorithm is the best algorithm which has been used for the bin packing problem. The First-Fit Algorithm is an example of a greedy approximation algorithm, in that the items will processed in any given order. The algorithm will place as many items as possible into the first bin, and then create a new bin if no other additional bins can be found. The process is then repeated for the rest of the items.
The First-Fit Algorithm has a approximation factor of 2 (APX). The approximation factor is used for NP-Hard problems, since it is very unlikely that a efficient algorithm will be produced to solve the problem directly, and therefore a P class algorithm can be developed in order to find a approximate answer. The approximation factor of 2, means that the algorithm will never use more than twice the number of least bins needed for the bin packing problem. For instance, if the number of bins needed was 2, then the algorithm will never use more than 4.
References:
Bin Packing Problem
Subscribe to:
Comments (Atom)