I'm still in a hiatus at the moment, but I may write the occasional blog post now and again (during the hiatus) like in this example. I will be giving a brief insight into the concept of Qubits which is the analogue to Classical Bits (1's and 0's). The only real difference between the two types, is that Qubits can be manipulated and controlled by the laws of Quantum Mechanics such as Superposition and Quantum Entanglement; the Spin states are also of great importance here since the control of the Spin will help create strings of information which are studied in Quantum Information Theory.
Before reading this post, I will assume you have some mathematical knowledge of Linear Algebra and Dirac Notation. Otherwise, I'll explain the concepts as a I write about the fundamentals of Qubits.
Firstly, let's look at the concept of Spin. Spin is a very important concept for Qubits. Spin is the angular momentum of a particle intrinsic (property of itself) to it's body. Spin is often regarded as a vector in three dimensional space, and being in the Up or Down state. The Down state has less energy in comparison to the Up state, and with Qubits, the Down state is usually set and then the Spin state will be changed to the Up state by electromagnetic radiation when necessary. The notation below represents a state vector called a Ket.
$$\vert A>$$
The Ket vector can be used to represent Spin states, and commonly denoted in the following form:
<u|A> for an Up state and <d|A> for a Down state. The lowercase a and d actually represent the probability amplitudes of the particle being in those two quantum states. Of course, the particle can be in a superposition of those two quantum states, but under observation this coherence is usually broken and the particle is measured as being in one quantum spin state. The probability amplitudes are typically complex numbers, which means they have a real part and imaginary part.
To gather the probability of spin we square these probability amplitudes to give the following notation:
$$\lvert d^2 \rvert$$ and $$\lvert u^2 \rvert$$ which will need to equal 1.
More specifically, the two quantum states are called basis vectors, and can be represented as |0> and |1>. Thee basis is simply all the possible vectors for a particular vector space. I will assume you will know the formal definition of a basis.
Another two important points are the Bloch Sphere and Quantum Entanglement. Quantum Entanglement means if we change the state of one particle then it will change the state of a another particle which is entangled with the first particle. This is a fundamental idea to Quantum Computing. It enables us to compute a larger number of bits simultaneously. For example, a Qubit has two basis states: |0> and |1>, or more correctly as: |00> and |11> since a Qubit can be in superposition of two states at once. Remember that when we measure or observe the state, it will be in one state. If we change one Qubit to |00> then the other Qubit will change to |00> too. There is equal probability of the Qubit being in the superposition of |00> or |11>.
A important point to remember is that, for every additional Qubit you add, the computing power in comparison to a Classical Computer is doubled like so:
$$2^n$$
n is the number of Qubits. If we had 3 Qubits, then classically this will be equivalent to 8 Classical Bits.
Typically, Qubits are represented as a Bloch Sphere, since Qubits exist in a two-dimensional Hilbert Space where only the superposition of two quantum states is possible. In later posts I will attempt to explain the Bloch Sphere in more depth.
This post was only supposed to be very introductory, and not go into depth about Qubits and Quantum Computation. In the future, I will build upon this post and go into more depth about Quantum Computation and other theoretical concepts.
Instead of allowing my blog to completely go 'dead', I've decided to write a short post regarding my hiatus which is going to be used to improve of knowledge mathematics related to physics and computer science. The reason being is because I plan to finally go to University this September/October and study for a degree in Computer Science, and then eventually a Ph.D since I would like to research into the theory of Quantum Computing. To make things easier for myself and to give me an advantage when I do hopefully go to University, I feel it's better to learn the Mathematics beforehand since they are so crucial for a real understanding of the concepts in Theoretical Computer Science and Physics; Theoretical Physics is very mathematically orientated.
At the moment, I'm doing Business at college which isn't exactly my intended career path, but I only chose the subject since the Mathematics courses and Computing courses (more like Microsoft Office) didn't teach anything relevant to what I needed to learn. For example, at my Sixth Form (I did one year before going to college), the Maths was very statistics orientated and didn't teach much else apart from that. The physics courses were only classical mechanics and split across two campuses (two different schools were merged into one due to financial and political reasons).
So, that leaves me in the position of learning everything at home, which I've done anyway with the knowledge expressed in this blog. In a few months time I should be posting again and contributing to forums. I'll still be active on Twitter if anyone follows me.
This is going to be a relatively long blog post, but I feel it may be useful since not much information is given on about how to find the IAT (Import Address Table) and EAT (Export Address Table) with WinDbg. There is some useful articles and blog posts on the subject, but I would like to add my own explanations and bring all the information together into one blog post. I'll start with a description of the purpose of the tables and their general structure.
The IAT is simply a array of pointers which are loaded by the Image Loader. The IAT is used primarily as form of a lookup table, which is used to call function present in other library modules (.DLLs). Since the executable module will not the the know memory addresses of the libraries and it's stored functions, it brings the in the purpose of the IAT. The IAT slots will be written with memory addresses by the linker.
The IAT is part of a larger data structure called the _IMAGE_IMPORT_DESCRIPTOR, which also contains another lookup table called the INT (Import Name Table), which is identical to the IAT.
The OriginalFirstThunk points to the Import Name Table and the FirstThunk points to the Import Address Table. We can find these in WinDbg, but it may take a little detective work to do so. We need to find the base address of the current image (executable module) and the address of the Import Directory, which is simple with the use of the !dh extension.
Using the dd command to dump the memory addresses of the Import Directory, we can see the relevant members mentioned earlier.
000220e8 is the address of the OriginalFirstThunk and the 00022330 is the address of the FirstThunk. Again, using the dd command we can dump these addresses using WinDbg.
The addresses shown are for the INT, and by using the dc command on one of the selected offsets with the base address, you will be able to view the name of the function. The current example didn't produce much, since the program I was using was a very small program with one or two libraries.
We can display similar information with the FirstThunk, and I personally prefer using the FirstThunk since we can use the ln command with the address to find the exact function, which will be displayed cleanly with WinDbg.
Using the ln command, we can see the similar function name which was roughly shown with the INT:
We can use the !dh extension to load the PE Header Sections for a desired module, and then view the address of the IAT.
As mentioned before, since the IAT is a array of pointers, we can use the dps command to dump pointers with symbol information if provided.
This is only a small subset of the IAT, you can adjust the number of functions dumped by changing the dps parameters.
Now, we need to explore the EAT which is going to be a little more difficult to explore using WinDbg than the IAT. The EAT works in the same way as the IAT, apart from the library will be exporting the functions to the image executable, in which the program will import into the IAT.
We need to investigate the Export Directory which is a IMAGE_EXPORT_DIRECTORY data structure, used in the following format:
The AddressOfFunctions is the field which we are most interested in since this is the EAT. It also contains the RVAs (Relative Virtual Address) of the exported functions to be used by the PE Loader.
The AddressOfNames and AddressOfNameOrdinals are loaded alongside each other, to provide a linkage between the address of the function and the name of the function. The AddressOfNames is a pointer to a array of function names, and the AddressOfNameOrdinals is a pointer to a array used to index into the AddressOfFunctions to obtain the addresses for the function names.
Going back to the Export Directory and WinDbg, we can dump the Export Directory using similar methods as before.
I've highlighted the important addresses from the IMAGE_EXPORT_DIRECTORY (Export Directory) structure. The 00051dc is the AddressOfFunctions, the AddressOfNames is the 000b672c and the 000b7c7c is the AddressOfNameOrdinals.
Using the dd command to dump the AddressOfFunctions array, and then using the da command to dump each element of the array, we can see which functions are stored there.
Now we can use the da command to dump the exported function.
We could repeat this process for every exported function, but that would take a considerable amount of time, and there are easier methods than using WinDbg.
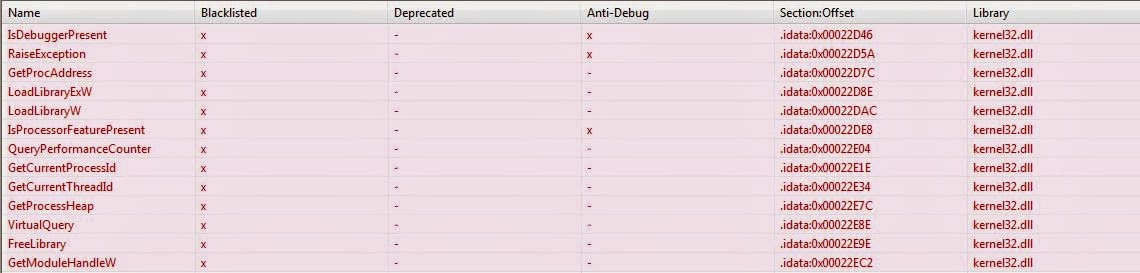
PeStudio can also be used to find the addresses of the IAT and EAT, and if these tables contain any functions. It also includes the size of the table.
Under the Imported Symbols, we can view the functions imported by the image executable, and if they potentially have a malicious intent. I've only shown the kernel32 based functions, since that was the library we were investigating using WinDbg.
We can view similar information with Dependency Walker, and selecting the desired library.
The columns are explained here.
In the future, I'll look into the other PE Header Sections and look at IAT Hooking.
Additional Reading and References:
Inside Windows: An In-Depth Look into the Win32 Portable Executable File Format Part 2
The NT Insider: Debugging Techniques: Take One...Give One
Win32 Assembly Tutorials
.gif)
.gif)
